|
The Keyboard Temperament of J. S. Bach
John Charles Francis, BSc (Hons), MSc, PhD
CH-3072 Ostermundigen, Switzerland
Francis@datacomm.ch
Introduction
Johann Sebastian Bach prepared his didactic Klavierbüchlein für Wilhelm Friedemann Bach in January 1720, following the tenth birthday of his oldest son, Wilhelm Friedemann. On its first pages, he described the clefs his son would encounter and the musical ornaments he would need, providing first an exercise with explicit fingering indications, the Applicatio (BWV 994), followed by a Preambulum (BWV 924). The intent of this latter piece, the second in Wilhelm Friedemann’s book, is considered in this paper. The thesis presented is that BWV 924 is nothing less than a pedagogic aid to help Wilhelm Friedemann perform keyboard tuning. It is shown how J. S. Bach’s keyboard temperament can be reconstructed from this piece.
Originally scattered throughout the old Bach-Gesamtausgabe (BGA), the Klavierbüchlein für Wilhelm Friedemann Bach was first published as a unit in 1962 under the auspices of the Neue Bach-Ausgabe (NBA) [1]. Around that time, a facsimile edition also became available [2]. Considerations regarding handwriting and the evolution of entries can be found in the NBA Critical Commentary [3]. The original manuscript is currently housed in the library of the Yale school of Music.
Johann Nikolaus Forkel, writing in 1802, noted that J. S. Bach always tuned his own keyboard and that the procedure did not take him more than fifteen minutes [4]. Andreas Sorge, commenting in 1748 on the tuning system of the renowned organ builder Gottfried Silbermann, mentioned Bach as having described four specific triads resulting from Silbermann’s method as having a barbaric nature intolerable to a good ear [1] [5]. An anecdote, in similar vein, was related by Edward John Hopkins in 1895, reporting a tradition whereby J. S. Bach as auditor of Silbermann’s instruments supposedly said “You tune the organ in the manner you please, and I play the organ in the key I please”; following his remark with a Fantasy in A-flat major causing Silbermann to retire to avoid his own “wolf” [2] [6]. Friedrich Wilhelm Marpurg, writing in 1776, related that J. S. Bach had confided his tuning method to a pupil, Kirnberger, who was expressly required to tune all the thirds sharp [3] [7].
In more recent times, Johann Sebastian Bach has been seen, on the one hand, as a pioneer of Equal Temperament [8] and, on the other, as a proponent of unequal Well Temperaments. In this latter regard, suggested temperaments have included those of Werckmeister [9] and Kirnberger [10]. Attempts at reconstructing Bach’s temperament have been made by Kellner [11] and Barnes [12].

Figure 1: Preambulum (BWV 924) from the Klavierbüchlein für Wilhelm Friedemann Bach
Decoding BWV 924
The Preambulum (BWV 924) is written in the key of C major and consists of eighteen measures (Figure 1). The bass line of the first three bars is shown in Figure 2.
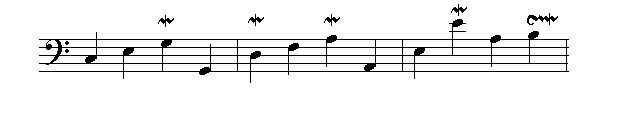
Figure 2: base line of BWV 924 (bars 1-3)
Of interest are the notes marked with trills [4], which, taken in order of occurrence preceded by the opening note, give rise to six consecutive notes on the circle of fifths C, G, D, A, E, B, with five corresponding intervals of a perfect fifth:
C - G, G - D, D - A, A - E, E - B
This observation motivates the following hypothesis: namely, that some of the trills in BWV 924 carry a meaning beyond the obvious one of musical ornamentation; their purpose being to serve as a memory aid for Wilhelm Friedemann Bach to help him recall the complex, yet fundamental, process of tuning a keyboard.
To proceed further some notational conventions are necessary: the opening C of BWV 924 will be denoted as C1, the note one octave below it as C0, the note one octave above as C2; the other notes within the octave will be similarly designated. With this notation in hand, the music in Figure 2 can be represented as follows:
C 1 E1 G1 G0 D1 F1 A1 A0 E1 E2 A1 B1
For reference purposes, certain notes have been underlined: namely those that fall on the circle of fifths and fall within one octave, the “tenor” octave [5]. Note, the two bolded notes are precisely those needed to construct and tune the underlined notes starting from C1. To illustrate this point, the tuning process is now described:
- Tune C1 to an external reference (where appropriate).
- Tune G1 using C1 as a reference (perfect fifth).
- Tune G0 using G1 as a reference (octave).
- Tune D1 using G0 as a reference (perfect fifth).
- Tune A1 using D1 as a reference (perfect fifth).
- Tune A0 using A1 as a reference (octave).
- Tune E1 using A0 as a reference (perfect fifth).
- Tune B1 using E1 as a reference (perfect fifth).
|
Interval |
Tuning |
Remarks |
|
C1 - G1 |
Just Fifth |
G1 indicated by trill |
|
G1 - G0 |
Octave |
Needed for next step |
|
G0 - D1 |
Just Fifth |
D1 indicated by trill |
|
D1 - A1 |
Just Fifth |
A1 indicated by trill |
|
A1 - A0 |
Octave |
Needed for next step |
|
A0 - E1 |
Just Fifth |
E1 indicated by trill |
|
E1 - B1 |
Just Fifth |
B1 indicated by trill |
Table 1: tuning of five consecutive perfect fifths on the circle of fifths
The assumption will be that Wilhelm Friedemann was taught to tune his fifths justly (i.e. pure); this assumption being motivated by several factors: the ease of tuning in just fifths [6], the rapidity with which this can be done [7], and the historical precedent of employing just fifths. The resulting tuning is summarised in Table 1.
Returning now to Figure 2 and keeping in mind the hypothesis that the trills embody a meaning for tuning purposes, it is observed that the trills are of two different kinds: the first four are mordants, while the latter is a, so-called, doppelt cadence u. mordant. For the time being, the focus will be on the four mordents; these being defined in the introductory table of ornaments that J. S. Bach included at the beginning of Wilhelm Friedemann’s Klavierbüchlein as indicated in Figure 3.
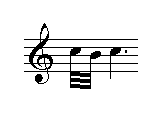
Figure 3: a mordant relates tonic and leading tone
From this, it follows that the four mordents occurring in the first three bars of BWV 924 (Figure 2), identify four relationships between tonic and leading tone, as shown in Table 2.
|
Mordent |
Diatonic Semitone Relationship |
|
G1 |
G1 - F1#
|
|
D1 |
D1 - C1#
|
|
A1 |
A1 - G1#
|
|
E2 |
E2 - D2#
|
Table 2: relationships implied by mordents
From the notes already tuned (Table 1), the leading notes in Table 2 must now be tuned. Since semitone relations cannot be tuned directly by ear with any useful accuracy, there is but one practical possibility: to tune by thirds. For the time being, the assumption will be to tune these thirds justly [8]; and under this condition the tuning shown in Table 3 can be derived. Note, it is possible, and indeed easier, to tune only one leading note from the third below and then proceed by tuning in perfect fifths as shown in Table 4 [9]. Using either of these equivalent procedures, the original circle of fifths in Table 1 is extended as shown in Table 5.
|
Note with Mordent |
Leading Tone |
Interval to Tune |
Tuning |
|
G1 |
F1#
|
D1 - F1#
|
Just Third |
|
D1 |
C1#
|
A0 - C1#
|
Just Third |
|
A1 |
G1#
|
E1 - G1#
|
Just Third |
|
E2 |
D2#
|
B1 - D2#
|
Just Third |
Table 3: tuning of the notes Bach marked by mordents as just thirds
|
Interval to Tune |
Tuning |
|
D1 - F1#
|
Just Third |
|
F1#
- F0#
|
Octave |
|
F0#
- C1#
|
Just Fifth |
|
C1#
- G1#
|
Just Fifth |
|
G1#
- D2#
|
Just Fifth |
Table 4: alternative method for tuning the notes Bach marked by mordents as just thirds
|
Interval |
Tuning |
|
C - G |
Just Fif |
|
G - D |
Just Fifth |
|
D - A |
Just Fifth |
|
A - E |
Just Fifth |
|
E - B |
Just Fifth |
|
B - F#
|
Wolf Interval |
|
F#
- C#
|
Just Fifth |
|
C #
- G#
|
Just Fifth |
|
G #
- D#
|
Just Fifth |
Table 5: extended circle of fifths
It can be observed that the second step of the tuning procedure dovetails nicely with the first, extending the circle of fifths by four steps. A further remark concerns the interval B - F#
, which was not tuned explicitly, but rather defined implicitly as a result of other tuning operations: this interval is a “wolf”, which needs to be dealt with. This is optimally achieved by spreading the wolf equally across the intervals:
A - E, E - B, B - F#
.
Note, that the tuning steps shown in Table 1 form part of the method of Pythagorean tuning, and so suffer from a perceived “defect”, namely, that the major thirds C1 - E1 and G1 - B1 are wide in comparison to the ideal of justly tuned thirds [10]. Accordingly, a prior, we might expect such notes to be tempered (narrowed) to remedy this problem; conveniently, distributing the wolf equally, also serves to narrow the thirds.
Returning now to the score of BWV 924 (Figure 1), and once again keeping in mind the hypothesis that the trills embody tuning instructions, it is observed that the notes B1 and E1 in bars 3 and 5, respectively, are marked by trills which Bach called doppelt cadence u. mordant. In view of the placement of this type of trill on precisely those notes that a priori need tempering to distribute the wolf and “improve” thirds, the doppelt cadence u. mordant on E1 and B1 is taken to imply a tempering operation. In this regard, note the shape of these trills: both of which point downwards, the direction in which the E1 and B1 must be tempered to distribute the wolf and improve the thirds. No guesswork is needed concerning the amount of this tempering, since the fundamental rationale for the operation is to distribute the wolf in Table 5 evenly, i.e., to adjust these two notes such that the error in the wolf interval B1- F2#
is spread evenly over the three [11] intervals A0- E1, E1- B1, B1- F2#
. This requirement precisely determines the tempering needed for E1 and B1, and after the relevant calculations are performed, the results indicated in Table 6 and Table 7 are obtained.
Returning again to the score of BWV 924 (Figure 1), it will be seen that the G1#
in bar 4 is also marked by a doppelt cadence u. mordant, but that it points upwards, not downwards. Earlier, the doppelt cadence u. mordant on E1 and B1 were taken to imply a narrowing of the thirds C1 - E1 and G1 - B1, and by analogy the inverted doppelt cadence u. mordant on G1#
can be interpreted as a widening of the interval E1 - G1#
. There are two ways such widening can be achieved:
- A lowering of E1: in this case the purpose of this doppelt cadence u. mordant is purely pedagogic; a lesson for Wilhelm Friedemann that narrowing the interval C1 - E1 has widened the interval E1 - G1#
.
- A prescriptive tuning instruction that the note G1#
should be raised, implying a widening of the interval C1#
- G1#
. To determine the amount of this tempering, note in Table 7 that the tempering narrowed each fifth by 1/3 of a syntonic comma. Accordingly, given the mirror-image appearance of the symbol, the fifth C1#
- G1#
should be widened by 1/3 syntonic comma, implying that G1#
should be sharpened by this amount [12].
Two semitones still remain to be specified, B@
and F respectively, there being no specific information from any trills in the score as to how the intervals should be tuned. Assuming tuning by just fifths, then starting at D#
/E@
the intervals E@
- B@
and B@
- F can be tuned. Alternatively, starting at C, the intervals F - C and B@
- F can be tuned in just fifths. In fact, it turns out that with the tuning steps considered so far, the difference is virtually imperceptible [13].
|
Note with doppelt cadence u. mordant |
Optimum Tempering |
|
B1 |
1/3 syntonic comma [14] downwards |
|
E1 |
2/3 syntonic comma downwards |
Table 6: optimum tempering to distribute the wolf
|
Interval |
Tempering |
|
A0 - E1 |
1/3 syntonic comma narrow |
|
E1 - B1 |
1/3 syntonic comma narrow |
|
B1 - F2#
|
1/3 syntonic comma narrow |
Table 7: the fifths resulting from tempering in Error! Reference source not found.
|
Interval to Tune |
Tuning |
|
B1 - B0 |
Octave |
|
B0 - F1#
|
Just Fifth |
|
F1#
- F0#
|
Octave |
|
F0#
- C1#
|
Just Fifth |
|
C1#
- G1#
|
Just Fifth |
|
G1#
- D2#
|
Just Fifth |
Table 8: method for tuning the notes Bach marked by mordents as sharp thirds
It is now shown how the tuning method above can be modified to tune the thirds in Table 4 wide, rather than justly. The procedure is as follows:
- Perform the tuning steps indicated in Table 1.
- Tune the interval D - F#
justly (as above).
- Temper the E and B such the three intervals A- E, E- B, B- F#
are equally good (as above).
- Retune F#
, such that the interval B - F#
is a just fifth [15] and continue tuning a just circle of fifths to D1#
/E@
(Table 8) [16].
- Reflecting the upward pointing doppelt cadence u. mordant on G1#
in BWV 924, widen the fifth C1#
- G1#
by 1/3 syntonic comma [17] (option, as above).
- Tune the B@
and F either i) as just fifths starting from D1#
/E@
, or ii) as just fifths starting from C[18].
The tuning systems considered so far are summarised in Table 10. The derived temperaments are referred to as Temperament I, Temperament II, Temperament III and Temperament IV, respectively. Their corresponding deviations from 12-tone Equal Temperament are given in Table 11, while a comparison between the fifths of all the derived temperaments is provided in Table 12. Thereafter, the characteristics of specific temperaments are described by tables of intervals, tables of thirds and fifths, and tables of the major and minor tetrachords.
Discussion
The structure of the sequence of fifths within the derived temperaments can be represented as shown in Table 9, where J, denotes a just fifth, N, a fifth narrowed by 1/3 syntonic comma, W, a fifth widened by 1/3 syntonic comma, E, an Equal Tempered fifth and X, the fifth that is 1/3 syntonic comma smaller than an Equal Tempered fifth.
Considering the major thirds of Temperament I (Table 14) and Temperament II (Table 18), it can be observed that the two narrowest major thirds are D - F#
and A - C#
, and that these are tuned justly. The widest occur at F#
- A#
and C#
- F, and are Pythagorean thirds, while the remaining thirds in Table 14 fall between these extremes in a progressive manner according to the circle of fifths. Looking now to the major (Table 15) and minor (Table 16) tetrachords for Temperament I, it will be noticed that duplication occurs: specifically, the major tetrachords starting on A@
and E@
are the same; likewise those starting on B@
and F. With regard to the minor tetrachords, the ones starting on B@
and F are identical. Comparing now with Temperament II, where, G#
/A@
has been sharpened, it can be observed that all tetrachords are unique (Table 19 and Table 20). This provides an excellent rationale for sharpening G#
/A@
, namely, to add explicit key colour and variety; a further rationale is the creation of a wide fifth which adds further colour to the temperament. A similar observation can be made regarding Temperament III: namely, that the major tetrachords on A@
and E@
are identical, as are those on B@
and F (Table 23). In the case of the minor tetrachords, there are also two duplications: those rooted in A@
and E@
are the same, and likewise those rooted in B@
and F (Table 24). Comparing now with Temperament IV, where explicit sharpening of G#
/A@
has occurred, it is important to note that all major (Table 27) and minor (Table 28) tetrachords have been rendered unique as a result of this tempering operation. That the tempering corresponding to the upward pointing doppelt cadence u. mordant should be exactly that needed to render all the tetrachords unique, is hardly a coincidence. Accordingly, the prescriptive interpretation of the trill on G#
/A@
in Figure 1 can be assumed. This eliminates Temperaments I and III from consideration.
By the above assumption, Temperaments II and IV remain as viable options. If the third-hand account by Friedrich Wilhelm Marpurg [7] is taken at face value: namely, that Kirnberger was expressly required by Bach to tune all the thirds sharp, then both Temperaments I and II must be rejected as invalid options. That would leave uniquely Temperament IV as the implied temperament. However, the possibility remains that Marpurg’s statement was merely a form of words to express Well Temperament. It is also possible that Marpurg misconstrued, or even misrepresented, Kirnberger’s remarks by implying that each and every fifth is tuned sharp. Alternatively, Bach may have taught Kirnberger a different tuning system to his own. Moreover, it is possible, that Wilhelm Friedemann may have used the simpler procedure of tuning the thirds justly, while his father adopted the expedient of tuning the thirds wide. It likewise conceivable, that J. S. Bach may have used different tuning variants at different stages of his career and in different situations. Moreover, if J. S. Bach is assumed to have derived the system embedded in BWV 924 himself, that suggests an experimental disposition. and accordingly, he may have used both of these variants at one time or another.
|
Temperament |
Structure |
|
I |
J J J N N N J J J J J E |
|
II |
J J J N N N J W N J J E |
|
III |
J J J N N J J J J J J X |
|
IV |
J J J N N J J W N J J X |
Table 9: structure of derived temperaments in terms of fifths
One final area of uncertainty to be addressed concerns the tuning of B@
and F, and whether they should these be tuned from E@
or C (or both). In the case, of Temperaments I and II, the choice is of little import, with a resulting difference in tuning of two cents. However, in the case of Temperaments III and IV, the difference is significant. The following options can be considered:
- Tune B@
justly from E@
, and then tune F justly from B@
; this is a valid option.
- Tune B@
justly from E@
; tune F justly from C; this option can be discounted as it gives rise to an inappropriate Pythagorean third on the interval B@
- D.
- Tune F justly from C and then tune B@
justly from F; this option can also be discounted as it gives rise to two inappropriately placed Pythagorean thirds on the intervals F - A and B@
- D.
- Tune F and B@
such that the intervals E@
- B@
, B@
- F, F – C are equal; this option compromises the just fifths unnecessarily and leads to an undulating pattern of widening thirds with two peaks. Accordingly, it can be discounted.
Temperaments I, II, III and IV have been compared with other historic temperaments and the results are shown in Figure 4, Figure 5, Figure 6, and Figure 7, respectively. Each figure indicates the calculated distance [19] of the historic temperament from the temperament derived from BWV 924, providing a measure of how far the historic temperament differs, on average, from those derived from BWV 924. The following observations apply to all the derived temperaments:
- Of the historic temperaments considered, Equal Temperament is by far the closest approximating temperament to Temperaments III and IV.
- Barnes temperament [12], derived from a statistical analysis of Bach’s Well Tempered Clavier [20], is a much closer approximation to each derived temperaments than Kellner’s temperament [11].
- Silbermann’s temperament [5], as might be expected, is far away from those derived from BWV 924.
- The temperaments of Kirnberger [10] and Werckmeister III [9] are likewise very distant.
Conclusions
This paper has reported the discovery by the author of several tuning systems derived from an analysis of BWV 924. These systems were determined under the assumption that BWV 924 was explicitly constructed by Johann Sebastian Bach to provide a pedagogic tuning aid for his young son, Wilhelm Friedemann; the purpose being to serve as a reminder of lessons already taught. Lack of information with regard to the exact teaching of J. S. Bach led to the range of candidate solutions [21], being considered.
Two possible interpretations with regard to tempering A@
/G#
were possible: one pedagogic (and arguably contrived), and the other prescriptive: the former corresponded to Temperaments I and III, the latter to Temperaments II and IV. It was found that explicitly sharpening G#
/A@
renders all major and minor tetrachords unique, and also offers the benefit of one wide fifth, adding colour and variety to the keys. The author notes, that in the case of Temperament IV, for example, the key of A@
, alluded to by Edward John Hopkins [6], is most charming. In general, the variety and colour introduced by sharpening G#
/A@
is very pleasing. The choice between Temperaments II and IV, depends on the credence given to the remark of Friedrich Wilhelm Marpurg [7]. Accepting Marpurg’s proposition, implies accepting Temperament IV.
The implications of this analysis will be relevant for musicians concerned with the historical informed performance practice of Bach’s music. The results obtained have shown that several historic temperaments, including Werckmeister and Kirnberger, are unlike those derived from BWV 924; the Kellner temperament is likewise very different. Equal Temperament is a viable performance option, but lacks the benefit of justly tuned fifths and key colour. Accordingly, musicians are invited to experiment with the temperaments presented in this paper, and Temperament 4 is recommended as the starting point.
|
Fifth |
Just Thirds |
Wide Thirds |
|
Temperament I |
Temperament II
(Tempered G#
/ A@
) |
Temperament III |
Temperament IV
(Tempered G#
/ A@
) |
|
C - G |
Just |
Just |
Just |
Just |
|
G - D |
Just |
Just |
Just |
Just |
|
D - A |
Just |
Just |
Just |
Just |
|
A - E |
Narrow by 1/3 syntonic comma |
Narrow by 1/3 syntonic comma |
Narrow by 1/3 syntonic comma |
Narrow by 1/3 syntonic comma |
|
E - B |
Narrow by 1/3 syntonic comma |
Narrow by 1/3 syntonic comma |
Narrow by 1/3 syntonic comma |
Narrow by 1/3 syntonic comma |
|
B - F#
B - G@
|
Narrow by 1/3 syntonic comma |
Narrow by 1/3 syntonic comma |
Just |
Just |
|
F#
- C#
G@
- D@
|
Just |
Just |
Just |
Just |
|
C #
- G#
D@
- A@
|
Just |
Wide by 1/3 syntonic comma |
Just |
Wide by 1/3 syntonic comma |
|
G #
- D#
A@
- E@
|
Just |
Narrow by 1/3 syntonic comma |
Just |
Narrow by 1/3 syntonic comma |
|
D#
- A#
E@
- B@
|
Just |
Just |
Just |
Just |
|
A#
- F
B@
- F |
Just |
Just |
Just |
Just |
|
(F - C) |
(Equal Tempered) |
(Equal Tempered) |
(Narrow by slightly more than 1/3 syntonic comma) [22] |
(Narrow by slightly more than 1/3 syntonic comma) [23] |
Table 10: derived temperaments based on tempering by 1/3 syntonic comma [24]
|
Note |
Just Thirds |
Wide Thirds |
|
Temperament I |
Temperament II
(Tempered G#
/ A@
) |
Temperament III |
Temperament IV
(Tempered G#
/ A@
)
|
|
C |
0
|
0 |
0 |
0 |
|
C#
/ D@
|
-8 |
-8 |
-1 |
-1 |
|
D |
4 |
4 |
4 |
4 |
|
D#
/ E@
|
-4 |
-4 |
3 |
3 |
|
E |
1 |
1 |
1 |
1 |
|
F |
0 (-2) |
0 (-2) |
7 |
7 |
|
F#
/ G@
|
-10 |
-10 |
-3 |
-3 |
|
G |
2 |
2 |
2 |
2 |
|
G#
/ A@
|
-6 |
1 |
1 |
8 |
|
A |
6 |
6 |
6 |
6 |
|
A#
/ B@
|
-2 (-4) |
-2 (-4) |
5 |
5 |
|
B |
-5 |
-5 |
-5 |
-5 |
Table 11: deviation of temperaments from Equal Temperament [25]
|
Interval |
Temperament I |
Temperament II |
Temperament III |
Temperament IV |
|
C - G |
702 |
702 |
702 |
702 |
|
G - D |
702 |
702 |
702 |
702 |
|
D - A |
702 |
702 |
702 |
702 |
|
A - E |
695 |
695 |
695 |
695 |
|
E - B |
695 |
695 |
695 |
695 |
|
B - F#
/ B - G@
|
695 |
695 |
702 |
702 |
|
F#
- C#
/ G@
- D@
|
702 |
702 |
702 |
702 |
|
C#
- G#
/ D@
- A@
|
702 |
709 |
702 |
709 |
|
G#
- D#
/ A@
- E@
|
702 |
695 |
702 |
695 |
|
D#
-A#
/ E@
- B@
|
702 |
702 |
702 |
702 |
|
A#
- F / B@
- F |
702 |
702 |
702 |
702 |
|
F - C |
700 |
700 |
693 |
693 |
Table 12: comparison of fifths
|
C |
C#
D@
|
D |
D#
E@
|
E |
F |
F#
G@
|
G |
G#
A@
|
A |
A#
B@
|
B |
C |
|
C |
0 |
1108 |
996 |
904 |
799 |
700 |
610 |
498 |
406 |
294 |
202 |
105 |
0 |
|
C#
/D@
|
92 |
0 |
1088 |
996 |
892 |
792 |
702 |
590 |
498 |
386 |
294 |
197 |
92 |
|
D |
204 |
112 |
0 |
1108 |
1003 |
904 |
814 |
702 |
610 |
498 |
406 |
308 |
204 |
|
D#
/E@
|
296 |
204 |
92 |
0 |
1095 |
996 |
906 |
794 |
702 |
590 |
498 |
401 |
296 |
|
E |
401 |
308 |
197 |
105 |
0 |
1101 |
1010 |
899 |
807 |
695 |
603 |
505 |
401 |
|
F |
500 |
408 |
296 |
204 |
99 |
0 |
1110 |
998 |
906 |
794 |
702 |
605 |
500 |
|
F#
/G@
|
590 |
498 |
386 |
294 |
190 |
90 |
0 |
1088 |
996 |
884 |
792 |
695 |
590 |
|
G |
702 |
610 |
498 |
406 |
301 |
202 |
112 |
0 |
1108 |
996 |
904 |
807 |
702 |
|
G#
/A@
|
794 |
702 |
590 |
498 |
393 |
294 |
204 |
92 |
0 |
1088 |
996 |
899 |
794 |
|
A |
906 |
814 |
702 |
610 |
505 |
406 |
316 |
204 |
112 |
0 |
1108 |
1010 |
906 |
|
A#
/B@
|
998 |
906 |
794 |
702 |
597 |
498 |
408 |
296 |
204 |
92 |
0 |
1103 |
998 |
|
B |
1095 |
1003 |
892 |
799 |
695 |
595 |
505 |
393 |
301 |
190 |
97 |
0 |
1095 |
|
C |
1200 |
1108 |
996 |
904 |
799 |
700 |
610 |
498 |
406 |
294 |
202 |
105 |
0 |
Table 13: Temperament I interval analysis
|
Root |
Minor 3rd |
Major 3rd |
Fifth |
|
C |
296 |
401 |
702 |
|
G |
296 |
393 |
702 |
|
D |
296 |
386 |
702 |
|
A |
294 |
386 |
695 |
|
E |
301 |
393 |
695 |
|
B |
308 |
401 |
695 |
|
F#
/ G@
|
316 |
408 |
702 |
|
C#
/ D@
|
308 |
408 |
702 |
|
G#
/ A@
|
301 |
406 |
702 |
|
D#
/ E@
|
294 |
406 |
702 |
|
A#
/ B@
|
294 |
406 |
702 |
|
F |
294 |
406 |
700 |
Table 14: Temperament I thirds and fifths
|
C |
202 |
G |
202 |
D |
204 |
A |
204 |
E |
197 |
B |
190 |
|
D |
204 |
A |
204 |
E |
197 |
B |
190 |
F#
|
190 |
C#
|
197 |
|
E |
197 |
B |
190 |
F#
|
190 |
C#
|
197 |
G#
|
204 |
D#
|
204 |
|
F |
99 |
C |
105 |
G |
112 |
D |
112 |
A |
112 |
E |
105 |
|
|
|
|
|
|
|
|
|
|
|
|
|
F#
|
190 |
D@
|
197 |
A@
|
204 |
E@
|
204 |
B@
|
204 |
F |
204 |
|
G#
|
204 |
E@
|
204 |
B@
|
204 |
F |
204 |
C |
202 |
G |
202 |
|
A#
|
204 |
F |
204 |
C |
202 |
G |
202 |
D |
204 |
A |
204 |
|
B |
97 |
G@
|
90 |
D@
|
92 |
A@
|
92 |
E@
|
92 |
B@
|
92 |
Table 15: Temperament I major tetrachords
|
C |
202 |
G |
202 |
D |
204 |
A |
204 |
E |
197 |
B |
190 |
|
D |
204 |
A |
204 |
E |
197 |
B |
190 |
F#
|
190 |
C#
|
197 |
|
E@
|
92 |
B@
|
92 |
F |
99 |
C |
105 |
G |
112 |
D |
112 |
|
F |
204 |
C |
202 |
G |
202 |
D |
204 |
A |
204 |
E |
197 |
|
|
|
|
|
|
|
|
|
|
|
|
|
F#
|
190 |
D@
|
197 |
A@
|
204 |
E@
|
204 |
B@
|
204 |
F |
204 |
|
G#
|
204 |
E@
|
204 |
B@
|
204 |
F |
204 |
C |
202 |
G |
202 |
|
A |
112 |
F@
|
105 |
C@
|
97 |
G@
|
90 |
D@
|
92 |
A@
|
92 |
|
B |
190 |
G@
|
190 |
D@
|
197 |
A@
|
204 |
E@
|
204 |
B@
|
204 |
Table 16: Temperament I minor tetrachords
|
C |
C#
D@
|
D |
D#
E@
|
E |
F |
F#
G@
|
G |
G#
A@
|
A |
A#
B@
|
B |
C |
|
C |
0 |
1108 |
996 |
904 |
799 |
700 |
610 |
498 |
399 |
294 |
202 |
105 |
0 |
|
C#
/D@
|
92 |
0 |
1088 |
996 |
892 |
792 |
702 |
590 |
491 |
386 |
294 |
197 |
92 |
|
D |
204 |
112 |
0 |
1108 |
1003 |
904 |
814 |
702 |
603 |
498 |
406 |
308 |
204 |
|
D#
/E@
|
296 |
204 |
92 |
0 |
1095 |
996 |
906 |
794 |
695 |
590 |
498 |
401 |
296 |
|
E |
401 |
308 |
197 |
105 |
0 |
1101 |
1010 |
899 |
799 |
695 |
603 |
505 |
401 |
|
F |
500 |
408 |
296 |
204 |
99 |
0 |
1110 |
998 |
899 |
794 |
702 |
605 |
500 |
|
F#
/G@
|
590 |
498 |
386 |
294 |
190 |
90 |
0 |
1088 |
989 |
884 |
792 |
695 |
590 |
|
G |
702 |
610 |
498 |
406 |
301 |
202 |
112 |
0 |
1101 |
996 |
904 |
807 |
702 |
|
G#
/A@
|
801 |
709 |
597 |
505 |
401 |
301 |
211 |
99 |
0 |
1095 |
1003 |
906 |
801 |
|
A |
906 |
814 |
702 |
610 |
505 |
406 |
316 |
204 |
105 |
0 |
1108 |
1010 |
906 |
|
A#
/B@
|
998 |
906 |
794 |
702 |
597 |
498 |
408 |
296 |
197 |
92 |
0 |
1103 |
998 |
|
B |
1095 |
1003 |
892 |
799 |
695 |
595 |
505 |
393 |
294 |
190 |
97 |
0 |
1095 |
|
C |
1200 |
1108 |
996 |
904 |
799 |
700 |
610 |
498 |
399 |
294 |
202 |
105 |
0 |
Table 17: Temperament II interval analysis
|
Root |
Minor 3rd |
Major 3rd |
Fifth |
|
C |
296 |
401 |
702 |
|
G |
296 |
393 |
702 |
|
D |
296 |
386 |
702 |
|
A |
294 |
386 |
695 |
|
E |
301 |
401 |
695 |
|
B |
308 |
401 |
695 |
|
F#
/ G@
|
316 |
408 |
702 |
|
C#
/ D@
|
308 |
408 |
709 |
|
G#
/ A@
|
294 |
399 |
695 |
|
D#
/ E@
|
294 |
406 |
702 |
|
A#
/ B@
|
294 |
406 |
702 |
|
F |
301 |
406 |
700 |
Table 18: Temperament II thirds and fifths
|
C |
202 |
G |
202 |
D |
204 |
A |
204 |
E |
197 |
B |
190 |
|
D |
204 |
A |
204 |
E |
197 |
B |
190 |
F#
|
190 |
C#
|
197 |
|
E |
197 |
B |
190 |
F#
|
190 |
C#
|
197 |
G#
|
211 |
D#
|
204 |
|
F |
99 |
C |
105 |
G |
112 |
D |
112 |
A |
105 |
E |
105 |
|
|
|
|
|
|
|
|
|
|
|
|
|
F#
|
190 |
D@
|
197 |
A@
|
211 |
E@
|
204 |
B@
|
197 |
F |
204 |
|
G#
|
211 |
E@
|
204 |
B@
|
197 |
F |
204 |
C |
202 |
G |
202 |
|
A#
|
197 |
F |
204 |
C |
202 |
G |
202 |
D |
204 |
A |
204 |
|
B |
97 |
G@
|
90 |
D@
|
92 |
A@
|
99 |
E@
|
92 |
B@
|
92 |
Table 19: Temperament II major tetrachords
|
C |
202 |
G |
202 |
D |
204 |
A |
204 |
E |
197 |
B |
190 |
|
D |
204 |
A |
204 |
E |
197 |
B |
190 |
F#
|
190 |
C#
|
197 |
|
E@
|
92 |
B@
|
190 |
F |
190 |
C |
197 |
G |
211 |
D |
204 |
|
F |
204 |
C |
105 |
G |
112 |
D |
112 |
A |
105 |
E |
105 |
|
|
|
|
|
|
|
|
|
|
|
|
|
F#
|
190 |
D@
|
197 |
A@
|
211 |
E@
|
204 |
B@
|
197 |
F |
204 |
|
G#
|
211 |
E@
|
204 |
B@
|
197 |
F |
204 |
C |
202 |
G |
202 |
|
A |
197 |
F@
|
204 |
C@
|
202 |
G@
|
202 |
D@
|
204 |
A@
|
204 |
|
B |
97 |
G@
|
90 |
D@
|
92 |
A@
|
99 |
E@
|
92 |
B@
|
92 |
Table 20: Temperament II minor tetrachords
|
C |
C#
D@
|
D |
D#
E@
|
E |
F |
F#
G@
|
G |
G#
A@
|
A |
A#
B@
|
B |
C |
|
C |
0 |
1101 |
996 |
897 |
799 |
693 |
603 |
498 |
399 |
294 |
195 |
105 |
0 |
|
C#
/D@
|
99 |
0 |
1095 |
996 |
899 |
792 |
702 |
597 |
498 |
393 |
294 |
204 |
99 |
|
D |
204 |
105 |
0 |
1101 |
1003 |
897 |
807 |
702 |
603 |
498 |
399 |
308 |
204 |
|
D#
/E@
|
303 |
204 |
99 |
0 |
1103 |
996 |
906 |
801 |
702 |
597 |
498 |
408 |
303 |
|
E |
401 |
301 |
197 |
97 |
0 |
1093 |
1003 |
899 |
799 |
695 |
595 |
505 |
401 |
|
F |
507 |
408 |
303 |
204 |
107 |
0 |
1110 |
1005 |
906 |
801 |
702 |
612 |
507 |
|
F#
/G@
|
597 |
498 |
393 |
294 |
197 |
90 |
0 |
1095 |
996 |
892 |
792 |
702 |
597 |
|
G |
702 |
603 |
498 |
399 |
301 |
195 |
105 |
0 |
1101 |
996 |
897 |
807 |
702 |
|
G#
/A@
|
801 |
702 |
597 |
498 |
401 |
294 |
204 |
99 |
0 |
1095 |
996 |
906 |
801 |
|
A |
906 |
807 |
702 |
603 |
505 |
399 |
308 |
204 |
105 |
0 |
1101 |
1010 |
906 |
|
A#
/B@
|
1005 |
906 |
801 |
702 |
605 |
498 |
408 |
303 |
204 |
99 |
0 |
1110 |
1005 |
|
B |
1095 |
996 |
892 |
792 |
695 |
588 |
498 |
393 |
294 |
190 |
90 |
0 |
1095 |
|
C |
1200 |
1101 |
996 |
897 |
799 |
693 |
603 |
498 |
399 |
294 |
195 |
105 |
0 |
Table 21: Temperament III interval analysis
|
Root |
Minor 3rd |
Major 3rd |
Fifth |
|
C |
303 |
401 |
702 |
|
G |
303 |
393 |
702 |
|
D |
303 |
393 |
702 |
|
A |
294 |
393 |
695 |
|
E |
301 |
401 |
695 |
|
B |
308 |
408 |
702 |
|
F#
/ G@
|
308 |
408 |
702 |
|
C#
/ D@
|
301 |
408 |
702 |
|
G#
/ A@
|
294 |
399 |
702 |
|
D#
/ E@
|
294 |
399 |
702 |
|
A#
/ B@
|
294 |
399 |
702 |
|
F |
294 |
399 |
693 |
Table 22: Temperament III thirds and fifths
|
C |
195 |
G |
195 |
D |
204 |
A |
204 |
E |
197 |
B |
190 |
|
D |
204 |
A |
204 |
E |
197 |
B |
190 |
F#
|
197 |
C#
|
204 |
|
E |
197 |
B |
190 |
F#
|
197 |
C#
|
204 |
G#
|
204 |
D#
|
204 |
|
F |
107 |
C |
105 |
G |
105 |
D |
105 |
A |
105 |
E |
97 |
|
|
|
|
|
|
|
|
|
|
|
|
|
F#
|
197 |
D@
|
204 |
A@
|
204 |
E@
|
204 |
B@
|
204 |
F |
204 |
|
G#
|
204 |
E@
|
204 |
B@
|
204 |
F |
204 |
C |
195 |
G |
195 |
|
A#
|
204 |
F |
204 |
C |
195 |
G |
195 |
D |
204 |
A |
204 |
|
B |
90 |
G@
|
90 |
D@
|
99 |
A@
|
99 |
E@
|
99 |
B@
|
99 |
Table 23: Temperament III major tetrachords
|
C |
195 |
G |
195 |
D |
204 |
A |
204 |
E |
197 |
B |
190 |
|
D |
204 |
A |
204 |
E |
197 |
B |
190 |
F#
|
197 |
C#
|
204 |
|
E@
|
99 |
B@
|
99 |
F |
107 |
C |
105 |
G |
105 |
D |
105 |
|
F |
204 |
C |
195 |
G |
195 |
D |
204 |
A |
204 |
E |
197 |
|
|
|
|
|
|
|
|
|
|
|
|
|
F#
|
197 |
D@
|
204 |
A@
|
204 |
E@
|
204 |
B@
|
204 |
F |
204 |
|
G#
|
204 |
E@
|
204 |
B@
|
204 |
F |
204 |
C |
195 |
G |
195 |
|
A |
105 |
F@
|
97 |
C@
|
90 |
G@
|
90 |
D@
|
99 |
A@
|
99 |
|
B |
190 |
G@
|
197 |
D@
|
204 |
A@
|
204 |
E@
|
204 |
B@
|
204 |
Table 24: Temperament III minor tetrachords
|
C |
C#
D@
|
D |
D#
E@
|
E |
F |
F#
G@
|
G |
G#
A@
|
A |
A#
B@
|
B |
C |
|
C |
0 |
1101 |
996 |
897 |
799 |
693 |
603 |
498 |
392 |
294 |
195 |
105 |
0 |
|
C#
/D@
|
99 |
0 |
1095 |
996 |
899 |
792 |
702 |
597 |
491 |
393 |
294 |
204 |
99 |
|
D |
204 |
105 |
0 |
1101 |
1003 |
897 |
807 |
702 |
595 |
498 |
399 |
308 |
204 |
|
D#
/E@
|
303 |
204 |
99 |
0 |
1103 |
996 |
906 |
801 |
695 |
597 |
498 |
408 |
303 |
|
E |
401 |
301 |
197 |
97 |
0 |
1093 |
1003 |
899 |
792 |
695 |
595 |
505 |
401 |
|
F |
507 |
408 |
303 |
204 |
107 |
0 |
1110 |
1005 |
899 |
801 |
702 |
612 |
507 |
|
F#
/G@
|
597 |
498 |
393 |
294 |
197 |
90 |
0 |
1095 |
989 |
892 |
792 |
702 |
597 |
|
G |
702 |
603 |
498 |
399 |
301 |
195 |
105 |
0 |
1093 |
996 |
897 |
807 |
702 |
|
G#
/A@
|
808 |
709 |
605 |
505 |
408 |
301 |
211 |
107 |
0 |
1103 |
1003 |
913 |
808 |
|
A |
906 |
807 |
702 |
603 |
505 |
399 |
308 |
204 |
97 |
0 |
1101 |
1010 |
906 |
|
A#
/B@
|
1005 |
906 |
801 |
702 |
605 |
498 |
408 |
303 |
197 |
99 |
0 |
1110 |
1005 |
|
B |
1095 |
996 |
892 |
792 |
695 |
588 |
498 |
393 |
287 |
190 |
90 |
0 |
1095 |
|
C |
1200 |
1101 |
996 |
897 |
799 |
693 |
603 |
498 |
392 |
294 |
195 |
105 |
0 |
Table 25: Temperament IV interval analysis
|
Root |
Minor 3rd |
Major 3rd |
Fifth |
|
C |
303 |
401 |
702 |
|
G |
303 |
393 |
702 |
|
D |
303 |
393 |
702 |
|
A |
294 |
393 |
695 |
|
E |
301 |
408 |
695 |
|
B |
308 |
408 |
702 |
|
F#
/ G@
|
308 |
408 |
702 |
|
C#
/ D@
|
301 |
408 |
709 |
|
G#
/ A@
|
287 |
392 |
695 |
|
D#
/ E@
|
294 |
399 |
702 |
|
A#
/ B@
|
294 |
399 |
702 |
|
F |
301 |
399 |
693 |
Table 26: Temperament IV thirds and fifths
|
C |
195 |
G |
195 |
D |
204 |
A |
204 |
E |
197 |
B |
190 |
|
D |
204 |
A |
204 |
E |
197 |
B |
190 |
F#
|
197 |
C#
|
204 |
|
E |
197 |
B |
190 |
F#
|
197 |
C#
|
204 |
G#
|
211 |
D#
|
204 |
|
F |
107 |
C |
105 |
G |
105 |
D |
105 |
A |
97 |
E |
97 |
|
|
|
|
|
|
|
|
|
|
|
|
|
F#
|
197 |
D@
|
204 |
A@
|
211 |
E@
|
204 |
B@
|
197 |
F |
204 |
|
G#
|
211 |
E@
|
204 |
B@
|
197 |
F |
204 |
C |
195 |
G |
195 |
|
A#
|
197 |
F |
204 |
C |
195 |
G |
195 |
D |
204 |
A |
204 |
|
B |
90 |
G@
|
90 |
D@
|
99 |
A@
|
107 |
E@
|
99 |
B@
|
99 |
Table 27: Temperament IV major tetrachords
|
C |
195 |
G |
195 |
D |
204 |
A |
204 |
E |
197 |
B |
190 |
|
D |
204 |
A |
204 |
E |
197 |
B |
190 |
F#
|
197 |
C#
|
204 |
|
E@
|
99 |
B@
|
99 |
F |
107 |
C |
105 |
G |
105 |
D |
105 |
|
F |
204 |
C |
195 |
G |
195 |
D |
204 |
A |
204 |
E |
197 |
|
|
|
|
|
|
|
|
|
|
|
|
|
F#
|
197 |
D@
|
204 |
A@
|
211 |
E@
|
204 |
B@
|
197 |
F |
204 |
|
G#
|
211 |
E@
|
204 |
B@
|
197 |
F |
204 |
C |
195 |
G |
195 |
|
A |
97 |
F@
|
97 |
C@
|
90 |
G@
|
90 |
D@
|
99 |
A@
|
107 |
|
B |
190 |
G@
|
197 |
D@
|
204 |
A@
|
211 |
E@
|
204 |
B@
|
197 |
Table 28: Temperament IV minor tetrachords
| |
Temperament 1 |
Temperament 2 |
Temperament 3 |
Temperament 4 |
|
Minor 2nd |
90 [26], 92 [27], 97, 99 [28], 105 [29], 112 [30] |
90, 92, 97, 99, 105, 112 |
90, 97, 99, 105, 107 |
90, 95, 97, 99, 105, 107 |
|
Major 2nd |
190, 197, 202, 204 |
190, 197, 202, 204, 211 |
190, 195, 197, 204 |
190, 195, 197, 204, 211 |
|
Minor 3rd |
294, 295, 301, 308, 316 |
294, 296, 301, 308, 316 |
294, 301, 303, 308 |
287, 294, 301, 303, 308 |
|
Major 3rd |
386 [31], 393 [32], 401, 406, 408 [33] |
386, 393, 399, 401, 406, 408 |
393, 399, 401, 408 |
392, 393, 399, 401, 408 |
|
Perfect 4th |
498, 500, 505 |
498, 491, 500, 505 |
498, 505, 507 |
491, 498, 505, 507 |
|
Aug. 4th / Dim. 5th |
590, 595, 597, 603, 605, 610 |
590, 595, 597, 603, 605, 610 |
588, 595, 597, 603, 605, 612 |
588, 595, 597, 603, 605, 612 |
|
Perfect 5th |
695, 700, 702 |
695, 700, 702, 709 |
693, 695, 702 |
693, 695, 702, 709 |
|
Minor 6th |
792, 794, 799, 807, 814 |
792, 794, 799, 801, 807, 814 |
792, 799, 801, 807 |
792, 799, 801, 807, 808 |
|
Major 6th |
884, 892, 899, 904, 906 |
884, 892, 899, 904, 906 |
892, 897, 899, 906 |
892, 897, 899, 906, 913 |
|
Minor 7th |
996, 998, 1003, 1010 |
996, 998, 1003, 1010 |
996, 1103, 1105, 1010 |
989, 996, 1003, 1005, 1010 |
|
Major 7th |
1088, 1095, 1101, 1103, 1108, 1110 |
1088, 1095, 1101, 1103, 1108, 1110 |
1093, 1095, 1101, 1103, 1110 |
1093, 1095, 1101, 1103, 1110 |
Table 29: sizes of intervals occurring in each temperament [34]
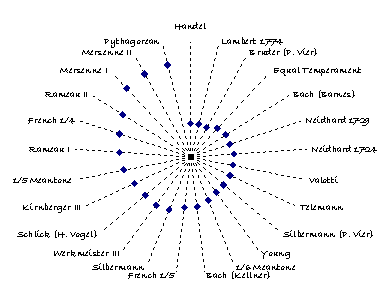
Figure 4: Temperament I comparison with historic temperaments [35]
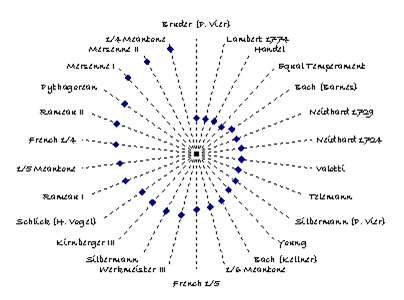
Figure 5: Temperament II comparison with historic temperaments
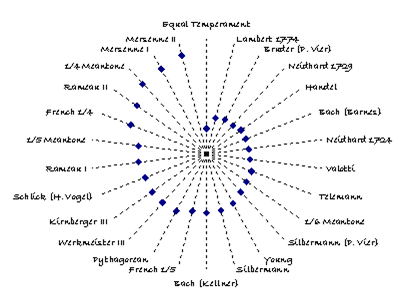
Figure 6: Temperament III comparison with historic temperaments
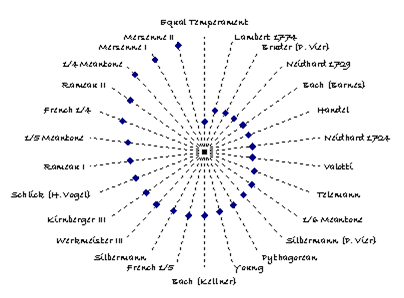
Figure 7: Temperament IV comparison with historic temperaments
Music Examples
See: Keyboard Temepramernt of J.S. Bach – Music Examples
References
|
[1] |
Bach, Johann Sebastian. Klavierbüchlein für Wilhelm Friedman Bach , Ed. Wolfgang Plath, B ärenreiter-Verlag Karl Vötterle GmbH & Co. KG, Kassel 1962. |
|
[2] |
Bach, Johann Sebastian. Clavier-Büchlein for Wilhelm Friedemann Bach, Edited in facsimile with a preface by Ralph Kirkpatrick. Yale University Press; London: Oxford Univ. Press 1959. N.Y.: Da Capo Press 1979. |
|
[3] |
Neue Bach-Ausgabe, Klavier- und Lautenwerke Band 5, Kritischer Bericht / Critical Commentary, B ärenreiter-Verlag Karl Vötterle GmbH & Co. KG, Kassel 1962., BA 5163. |
|
[4] |
Forkel, Johann Nikolaus, Ueber Johann Sebastian Bachs Lebens, Kunst und Kunstwerke, Leipzig. 1802; facs. ed., Frankfurt, 1950; English trans., London 1820. |
|
[5] |
Bach-Dokumente II, no. 575. |
|
[6] |
Hopkins, Edward John. The Organ, London, 1845, p.143. |
|
[7] |
Bach-Dokumente III, no. 815. |
|
[8] |
Barbour, J. Murray. Bach and the Art of the Temperament, Musical Quarterly, XXXIII (January, 1947), 64-89. |
|
[9] |
Werckmeister, Andreas. Musicalische Temperatur, Quedlinburg 1691.
Rudolf Rasch, ed. Tuning and Temperament Library, Vol. I. Utrecht: The Diapason Press, 1983. |
|
[10] |
Mekiel, Joyce. The Harmonic Theories of Kirnberger and Marpurg, Journal of Music Theory IV (November 1960), 169-193. |
|
[11] |
Kellner, Herbert Anton. A Mathematical Approach Reconstituting J. S. Bach's Keyboard Temperament, Bach X (1979), 2-9. |
|
[12] |
Barnes, John. Bach's Keyboard Temperament: Internal Evidence from the Well-Tempered Clavier, Early Music VII (April, 1979), 236 - 249. |
Footnotes
[1] „In denen vier schlimmen Triadibus aber ist ein rauhes, wildes, oder, wie Herr Kapellmeister Bach in Leipzig redet, ein barbarisches Wesen enthalten, welches einem guten Gehör unerträglich fällt“
[2] In the terminology of tuning, a “wolf” is an interval that is out of tune and metaphorically howls.
[3] „alle grossen Terzen scharf“
[4] The fourteen trills in BWV 924 are perhaps indicative of Bach’s personal signature, since according to the principles of Gematria, the name Bach is represented by the number 14 (B A C H = 2 + 1 + 3 + 8 = 14).
[5] The tenor octave is, incidentally, the area where the tension of the strings of a harpsichord is greatest; the practical corollary being that this octave should be tuned before others.
[6] It is relatively straightforward to tune two notes so that they are a just fifth apart, the procedure being to approximate the fifth and then tune to eliminates beats between the notes. Next to tuning in unisons and octaves, this is the most elementary of tuning procedures.
[7] Forkel’s observation regarding the maximum 15 minute keyboard tuning period needed by Bach motivates consideration of simple, rapid, procedures.
[8] The alternative hypothesis that the thirds were tuned wide is considered later in the paper.
[9] This simpler method is possible because the reference notes for tuning purposes ( Table 1) are separated by justly tuned fifths. It is a matter of conjecture which method was taught to Wilhelm Friedemann. In fact, all the notes needed to tune each third individually are already tuned, and to explicitly tune each interval in thirds would certainly have provided needed practice with the method, while avoiding the requirement for the young Wilhelm Friedemann to tune a circle of fifths in remote keys. However, if the alternative hypothesis that the thirds should be tuned sharp is entertained, then almost certainly but one third would be explicitly tuned, and the remaining notes tuned by fifths.
[10] While the Pythagorean third was considered consonant by Bach’s time, it still lay at the limit of acceptability and, accordingly, was often banished to remote keys.
[11] When the wolf is distributed over A0 : E1, E1 : B1, B1 : F2#., each of the intervals contains only 1/3 of the error that was originally present in the interval B1 : F2#, and this small amount is no longer a problem for the ear.
[12] Equivalently, the interval G1# - D1# should be narrowed by 1/3 syntonic comma.
[13] Around two cents.
[14] The syntonic comma is the interval between two notes of frequency ratio 81:80, or around 21 cents (1200 cents is an octave). It is defined as the difference between the interval of four contiguous just perfect fifths and the interval of two octaves and a just major third. A just perfect fifth has notes with a frequency ratio of 3:2 which is approximately 702 cents, and four of them are roughly 2807 cents. A just major third has notes with a frequency ratio of 5:4, which is equal to approximately 386 cents, implying that two octaves and a major third are about 2786 cents. The difference is around 21 cents.
[15] Alternatively, tune F1# such that the interval F1# - B1 is a just fourth. In either case, the effect is to widen the third D1 - F1# by 1/3 syntonic comma.
[16] If the first option of step 6 is assumed, continue tuning a just circle of fifths until F.
[17] Equivalently, narrow the interval G1# - D1#
by 1/3 syntonic comma (i.e., similar tempering to other tempered fifths).
[18] These tuning choices yield significantly different results. Later in the paper, it is determined which option is the correct one.
[19] For the purposes of this comparison, all temperaments were normalised to C and a Euclidian metric defined by taking the square root of the sum of the squares of the deltas for each note.
[20] Barnes statistical method does not claim to exactly reproduce Bach’s temperament, but rather to approximate it.
[21] Alternatives, based on reversing the sequence of tuning operations derived from BWV 924 have not been presented in this paper. Such options have been analysed, however, but led to less satisfactory results.
[22] This interval is tuned implicitly, of course.
[23] About 2 cents more in fact.
[24] Table 11 shows alternative tunings for F and Bb.
[25] The values in curved brackets are obtained by tuning F justly from C and Bb justly from F.
[26] Diatonic semitone of ratio 256 : 243 in Pythagorean tuning (Limma).
[27] Chromatic semitone of ratio 135 : 128 in Just Intonation and interval C# - D in Pythagorean tuning.
[28] Diatonic semitone F# - G in Pythagorean tuning.
[29] Chromatic semitone F - F# in Pythagorean tuning.
[30] Diatonic semitone of ratio 16:15 in Just Intonation.
[31] Major third of ratio 5 : 4 in Just Intonation.
[32] Major third of ratio 18/55.
[33] Pythagorean 3rd.
[34] The comments provided on this table are not intended to be complete!
[35] The centre of the figure denotes the temperament derived from BWV 924, and the distance from the centre is a measure of the fit of the historic temperament from that derived from BW924.
Feedback to the
Article
Written by Charles Francis (June 2004) ©
Contributed by Charles Francis (July 2004)
|